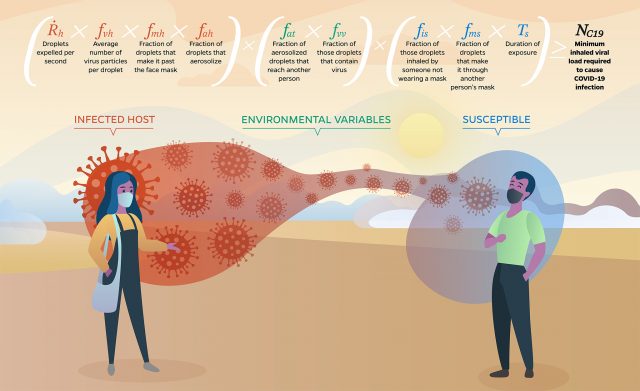
The Contagion Airborne Transmission inequality can be used to calculate the risk of airborne transmission of respiratory infections. Transmission occurs if the droplets expelled per second times the average number of virus particles per droplet, times the fraction of droplets that make it past the face mask, times the fraction of droplets that aerosolize, times the fraction of aerosolized droplets that reach another person, times the fraction of those droplets that contain virus, times the fraction of droplets inhaled by someone not wearing a mask, times the fraction of droplets that make it through another person’s mask, times the duration of exposure is greater than or equal to the minimum inhaled viral load required to cause infection. Graphic courtesy of Marissa Lanterman/Johns Hopkins University
OXFORD, Miss. – As researchers around the world race to answer unknowns about COVID-19, a University of Mississippi professor has helped create a mathematical framework to better understand how the coronavirus spreads.
Wen Wu, an assistant professor of mechanical engineering, worked with two professors at Johns Hopkins University to develop a mathematical model to estimate the risk of airborne transmission of respiratory infections such as COVID-19.
The model also shows how preventive measures such as wearing masks and physical distancing protect people from transmission, and how environmental variables affect the transmission of the coronavirus.
“The equation calculates the number of viable (infectious) droplets inhaled by susceptible people by multiplying several parameters,” said Wu, who joined the Ole Miss faculty in February 2020. “If the obtained number exceeds the infectious dose, the airborne transmission is established.”
Known as the Contagion Airborne Transmission, or CAT, inequality, the formula was first published in the Oct. 7 edition of the journal Physics of Fluids.
Co-authors on the paper are Rajat Mittal and Charles Meneveau, professors of mechanical engineering at Johns Hopkins University. The pair served as Wu’s advisers when he worked there as a postdoctoral researcher from 2017 to 2020.
The group’s paper contains several findings beyond the easily understood CAT inequality formula, Wu said. It also determines how protection from transmission increases with physical distancing and more.
“So, if you double your distance, you generally double your protection,” he said. “This kind of scaling or ‘rule’ would help inform policy. We also show that even simple cloth face masks provide significant protection and could reduce the spread of this disease.
“And we show that any physical activity that increases the breathing rate and volume of people will enhance the risk of transmission. This has important implications for the reopening of schools, malls, gyms, etc.”
While COVID-19’s transmission pathways are still being studied, it is understood that the virus is mostly spread person to person through the air, with people becoming infected after breathing in minuscule respiratory droplets produced by an infected person sneezing, coughing, breathing, yawning, singing or talking.
But several factors, including environmental variables, influence how these actions transmit the virus from person to person.
The CAT inequality offers a mathematical means for determining a person’s chances of catching COVID-19 under different scenarios. The model also applies to respiratory infections beyond COVID-19, including influenza, chickenpox, mumps, measles, whooping cough, tuberculosis, diphtheria and even the common cold.

Wen Wu, a UM assistant professor of mechanical engineering, has helped develop a mathematical formula to estimate the risk of airborne transmission of a respiratory infection such as COVID-19. Submitted photo
“Since researchers spanning different fields are studying COVID-19 from various perspectives, the mathematical framework serves as a common basis for scientific inquiry across disciplinary boundaries,” Wu said.
“It also serves as a tool to more easily communicate the factors associated with the spread of this disease to a wide range of stakeholders, including nonscientists such as policymakers, public media and the public at large. Given the rapidly evolving nature of the pandemic, the importance of clear communication of infection risk is more important than ever.”
A simple mathematical risk model that is comprehensible is important for bridging the gap between the research community and the general public.
“There’s still much confusion about the transmission pathways of COVID-19,” Mittal said in a Johns Hopkins press release. “This is partly because there is no common ‘language’ that makes it easy to understand the risk factors involved. What really needs to happen for one to get infected?
“If we can visualize this process more clearly and in a quantitative manner, we can make better decisions about which activities to resume and which to avoid.”
The trio was motivated to develop the CAT inequality model by the Drake Equation, “a conceptual framework to predict the number of technological civilizations that may exist in our galaxy” first conceived in 1961 by Frank Drake, an astronomer and astrophysicist involved in the search for extraterrestrial intelligence.
“The power of (the Drake Equation) is not in the fact that it actually allows us to predict this number with a known level of certainty, but in the fact that it provides an easy-to-understand framework for grasping the key factors involved in something that seems inestimable: the number of advanced life forms that exist elsewhere in our galaxy,” the trio wrote in their paper.
Wu’s research interests span from understanding and modeling turbulence to complexity in fluid mechanics, so working with other fluid mechanics experts to create the CAT inequality model follows his earlier work in the discipline.
“The profound beauty of the motion of fluid has captured my fancy for most of my life,” Wu said. “The complexity and dynamic motion of turbulence make these flows fascinating, even mesmerizing, to watch.
“Humans are a pattern-seeking species. I like to seek order in apparent chaos, and this, perhaps, is what makes turbulence such a captivating subject for me in the first place.”